Fast Fourier Transform (FFT)#
The following gives background information that is helpful to understand how the Fast Fourier Transform (FFT) and the corresponding normalizations are defined in pyfar and how these are related to the concepts of energy and power signals as well as their handling in arithmetic operations.
FFT Definition#
The discrete Fourier spectrum of an arbitrary, but band-limited signal \(x(n)\) is defined as
using a negative sign convention in the transform kernel \(\kappa(\mu, n) = e^{-i 2 \pi \mu \frac{n}{N}}\). Analogously, the discrete inverse Fourier transform is implemented as
Pyfar uses a DFT implementation for purely real-valued time signals resulting in Fourier spectra with complex conjugate symmetry for negative and positive frequencies \(X(\mu) = X(-\mu)^*\). As a result, the left-hand side of the spectrum is discarded, yielding \(X_R(\mu) = X(\mu) \mbox{ }\forall 0 \le \mu \le N/2\). Complex valued time signals can be implemented, if required.
FFT Normalizations#
Pyfar implements five normalizations [1] that can be applied to spectra after
the DFT. The normalizations are implicitly used by the
Signal
class and are available from normalization. For a
Signal object signal, signal.freq contains the normalized spectrum
according to signal.fft_norm and signal.freq_raw contains the raw
spectrum without any normalization. The time signals do not change regardless
of the normalization.
In order to illustrate the meaning of the normalizations, [1] is summarized and the consequences are discussed with respect to (arithmetic) operations.
Definitions
Norm |
Equation |
|---|---|
|
– |
|
\(X_{\text{SS}}(k) = \left\{\begin{array}{ll} X(k) & \forall k=0, k=\frac{N}{2}\\ 2 X(k) & \forall 0<k< \frac{N}{2} \end{array}\right.\) |
|
\(\overline{X}_{\text{SS}}(k) = \frac{1}{N} X_{\text{SS}}(k)\) |
|
\(\overline{X}_{RMS}(k) = \left\{\begin{array}{ll} \frac{1}{\sqrt{2}} \overline{X}_{\text{SS}}(k) & \forall 0<k< \frac{N}{2}\\ \quad \overline{X}_{\text{SS}}(k) & \forall k=0, k=\frac{N}{2} \end{array}\right.\) |
|
\(\overline{\overline{X}}_{\text{SS}}(k) = \lvert \overline{X}_{\text{RMS}}(k) \lvert ^2\) |
|
\(\overline{\overline{\underline{X}}}_{\text{SS}}(k) = \frac{N}{f_s} \overline{\overline{X}}_{\text{SS}}(k) = \frac{N}{f_s} \lvert \overline{X}_{\text{RMS}}(k) \lvert ^2\) |
Note that all pyfar signals are real-valued, leading to single-sided spectra \(X_{\text{SS}}(k)\). So there are small differences in the definitions compared to the formulas written in [1].
Explanations
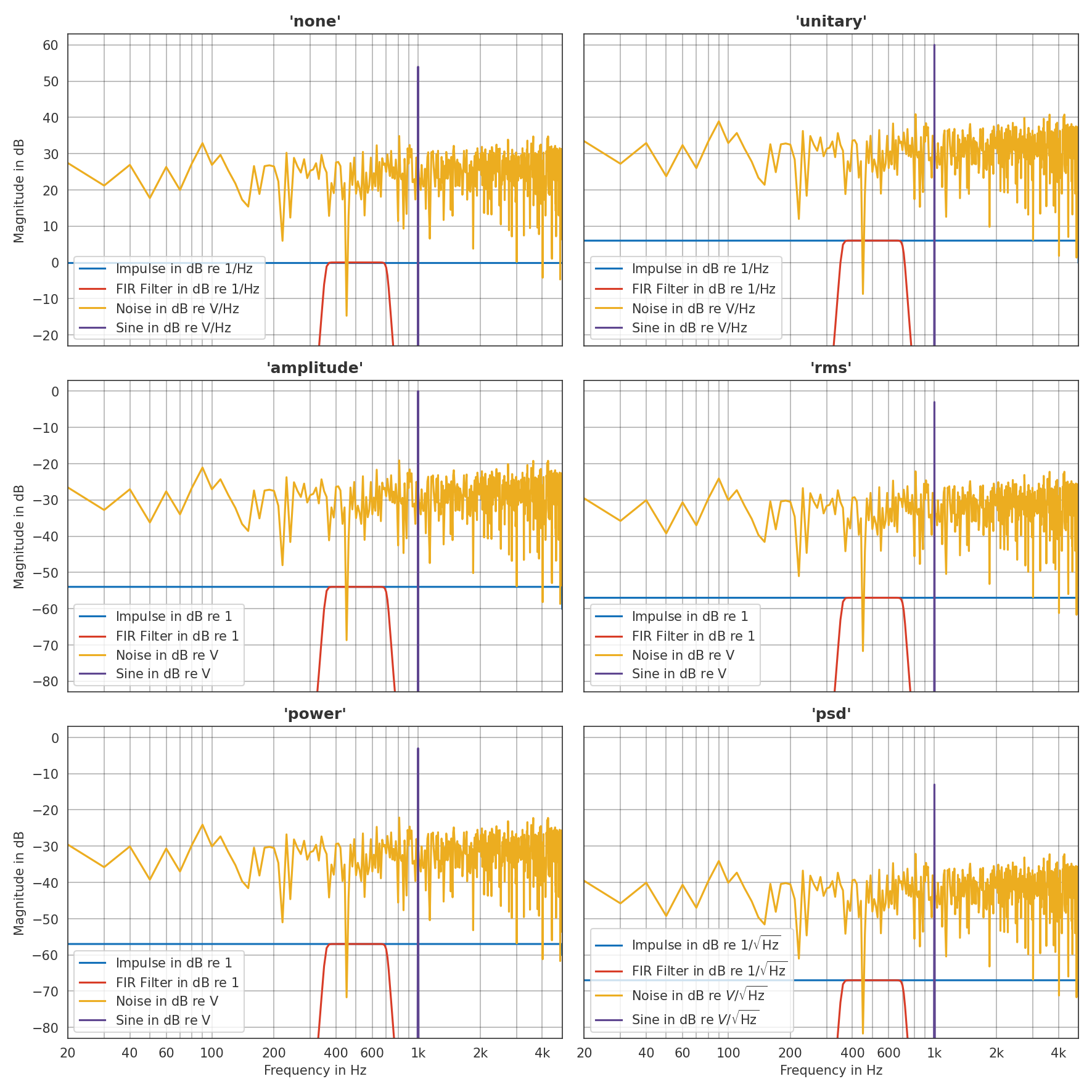
'none':Use the spectrum as it is. This norm is to be used for energy signals such as impulse responses. In this case the spectrum is independent from the signal length. For power signals, the spectrum depends on the number of samples (“longer signal = more energy”). In this case different normalizations are appropriate.
'unitary':Multiply the spectrum with a factor of 2 in order to represent power related measures correctly (e.g., the amplitude or RMS-value, see below). All following normalizations make use of this.
'amplitude':Normalize the spectrum to show the amplitude of the pure tone components contained in a signal. If the signal is a sine with an amplitude of 1, the spectrum will have an absolute value of 1 (0 dB) at the frequency of the sine.
'rms':Normalize the spectrum to show the RMS value of the pure tone components contained in a signal. If the signal is a sine with an amplitude of 1, the spectrum will have an absolute value of \(1/\sqrt{2}\) (-3 dB) at the frequency of the sine.
'power':In a dB representation, it equals the
'rms'normalization describing a power quantity. For stochastic broadband signals, this results in a dependence of the magnitude on the sampling rate as these are defined by a constant power density (see'psd').
'psd':Using this normalization, signals are represented as power densities (e.g. in V²/Hz), leading to a meaningful representation for broadband stochastic signals independent of the sampling rate.
Appropriate FFT Normalizations
Signal type |
Variation |
Normalization |
|---|---|---|
Energy |
Impulse responses |
|
Power |
Discrete tones |
|
Power |
Broadband stochastic signals |
|
Examples
Four signals with a length of 1000 samples and a sampling rate of 10 kHz are used for illustration:
An impulse (\(x(0)=1\) and zero otherwise) with a constant spectrum. This is an energy signal, so the appropriate normalization is
'none'.A fractional octave FIR filter presenting a system with finite energy (e.g., a loudspeaker transfer function, a room impulse response, an HRTF …) It is an energy signal, so the appropriate normalization is
'none'.A sine signal with an amplitude of \(1 \text{V}\). It represents a discrete tone of which a snippet was recorded. Accordingly, it possess a finite power but infinite energy and is a power signal with appropriate normalizations
'amplitude','rms', or'power'.A white noise signal with an RMS value of \(1/\sqrt{2} \text{V}\). It represents a broadband stochastic signal of which a snippet was recorded of. Accordingly, it is a power signal with the appropriate normalization
'psd'.
Note that the implied units differ and a prefix of 10 is used for the dB
calculations of the normalizations 'power' and 'psd'.
The
'none'normalization gives the expected results for the impulse and FIR filter, but leads to a magnitude of number of samples/2 for the sine signal (1000/2, 60-6 dB). As illustrated, other normalizations than'none'are not meaningful for the IRs.For the sine signal,
'unitary'normalization considers the factor 2 due to the single-side spectrum (+6 dB compared to'none'). The'amplitude'normalization considers the number of samples, so the amplitude of 1 V (= 0 dB) is represented in the spectrum. Accordingly, the magnitude of the sine is -3 dBV with'rms'and'power'normalization.With
'psd'normalization, the sine’s magnitude is reduced by a factor of number of samples / sampling rate (1/10, -10 dB). As discussed above, this normalization is only meaningful for the noise, as is represents a spectral density.
For further details, especially on the the background for the power normalizations, it is referred to [1].
References
See fft for a complete documentation.