Coordinates

The following introduces the concept of the coordinates class and the coordinate systems that are available in pyfar.

Coordinates Class

Different coordinate systems are frequently used in acoustics research and handling sampling points and different systems can be cumbersome. The Coordinates class was designed with this in mind. It can convert between coordinate systems and rotate, query and plot coordinates points. Functions for converting coordinates not stored in a Coordinates object are available for convenience. However, it is strongly recommended to use the Coordinates class for all conversions.

Coordinate Systems

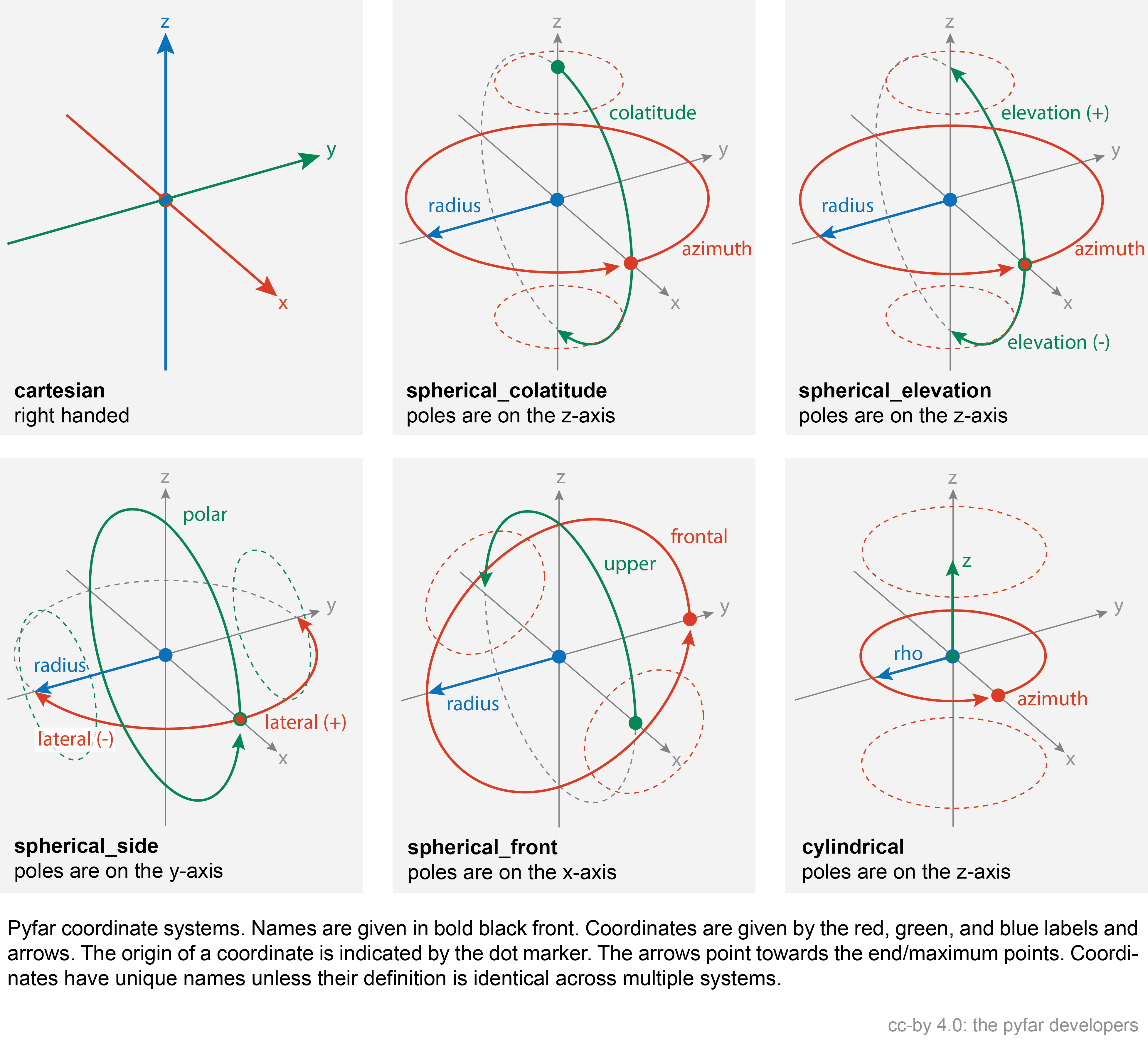
Coordinate systems are defined by their domain (e.g. 'spherical'), convention (e.g. 'top_elev'), and unit (e.g. 'deg'). The available coordinate systems are shown in the image below

The unit for length is always meter, while the unit for angles is radians. For more details see the table below.

Coordinate	Descriptions
x, y, z	x, y, z coordinate of a right handed Cartesian coordinate system in meter (\(-\infty\) < x,y,z < \(\infty\)).
azimuth	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and so on (\(-\infty\) < azimuth < \(\infty\), \(2\pi\)-cyclic).
elevation	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive z-direction, \(\pi/2\) radians in positive x-direction, and \(\pi\) in negative z-direction (\(\pi/2\) < elevation < \(\pi/2\)). The elevation is a variation of the elevation angle.
colatitude	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians colatitude are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(-\pi/2\) in negative z-direction (\(0\) < colatitude < \(\pi\)). The colatitude is a variation of the colatitude.
lateral	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and \(-\pi/2\) in negative y-direction (\(-\pi/2\) < lateral < \(\pi/2\)).
polar	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative x-direction and so on (\(-\infty\) < polar < \(\infty\), \(2\pi\)-cyclic).
frontal	Angle in the y-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive y-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative y-direction and so on (\(-\infty\) < frontal < \(\infty\), \(2\pi\)-cyclic).
upper	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(\pi\) in negative x-direction (\(0\) < upper < \(\pi\)).
radius	Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).
rho	Distance perpendicular to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).

Samplings

A plethora of sampling schemes to generate coordinate objects is contained in samplings.