Coordinates#

The following introduces the Coordinates class and the coordinate systems that are available in pyfar. Available sampling schemes are listed at spharpy.samplings. Examples for working with Coordinates objects are part of the pyfar gallery.

Different coordinate systems are frequently used in acoustics research and handling sampling points and different systems can be cumbersome. The Coordinates class was designed with this in mind. It stores coordinates in cartesian coordinates internally and can convert to all coordinate systems listed below. Additionally, the class can query and plot coordinates points. Addition and subtraction are supported with numbers and Coordinates objects, while multiplication and division are supported with numbers only. All arithmetic operations are performed element-wise on Cartesian coordinates using the appropriate operator. Functions for converting coordinates not stored in a Coordinates object are available for convenience. However, it is strongly recommended to use the Coordinates class for all conversions.

Coordinate Systems#

Each coordinate system has a unique name, e.g., spherical_elevation, and is defined by three coordinates, in this case azimuth, elevation, and radius. The available coordinate systems are shown in the image below.

Coordinates#

The unit for length for the coordinates is always meter, while the unit for angles is radians. Each coordinate is unique, but can appear in multiple coordinate systems, e.g., the azimuth angle is contained in two coordinate systems (spherical_colatitude and spherical_elevation). The table below lists all coordinates.

Coordinate	Descriptions
`x`, `y`, `z`	x, y, z coordinate of a right handed Cartesian coordinate system in meter (\(-\infty\) < x,y,z < \(\infty\)).
`azimuth`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and so on (\(-\infty\) < azimuth < \(\infty\), \(2\pi\)-cyclic).
`colatitude`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians colatitude are defined in positive z-direction, \(\pi/2\) radians in positive x-direction, and \(\pi\) in negative z-direction (\(0\leq\) colatitude \(\leq\pi\)). The colatitude is a variation of the elevation angle.
`elevation`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(-\pi/2\) in negative z-direction (\(-\pi/2\leq\) elevation \(\leq\pi/2\)). The elevation is a variation of the colatitude.
`lateral`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and \(-\pi/2\) in negative y-direction (\(-\pi/2\leq\) lateral \(\leq\pi/2\)).
`polar`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians polar angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative x-direction and so on (\(-\infty\) < polar < \(\infty\), \(2\pi\)-cyclic).
`frontal`	Angle in the y-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians frontal angle are defined in positive y-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative y-direction and so on (\(-\infty\) < frontal < \(\infty\), \(2\pi\)-cyclic).
`upper`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians upper angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(\pi\) in negative x-direction (\(0\leq\) upper \(\leq\pi\)).
`radius`	Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).
`rho`	Radial distance to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).

Classes:

Coordinates([points_1, points_2, points_3, ...])

This function will be changed in pyfar 0.8.0 and will just be able to get cartesian coordinates.

Functions:

`cart2cyl`(x, y, z)	Transforms from Cartesian to cylindrical coordinates.
`cart2sph`(x, y, z)	Transforms from Cartesian to spherical coordinates.
`cyl2cart`(azimuth, height, radius)	Transforms from cylindrical to Cartesian coordinates.
`sph2cart`(azimuth, colatitude, radius)	Transforms from spherical to Cartesian coordinates.

`cross`(a, b)	Cross product of two Coordinates objects.
`deg2rad`(coordinates[, domain])	Convert a copy of coordinates in degree to radians.
`dot`(a, b)	Dot product of two Coordinates objects.
`rad2deg`(coordinates[, domain])	Convert a copy of coordinates in radians to degree.

class pyfar.Coordinates(points_1: array = array([], dtype=float64), points_2: array = array([], dtype=float64), points_3: array = array([], dtype=float64), domain: str = 'cart', convention: str = None, unit: str = None, weights: array = None, sh_order=None, comment: str = '')[source]#

This function will be changed in pyfar 0.8.0 and will just be able to get cartesian coordinates. If you want to initialize in an other domain use from_spherical_colatitude, from_spherical_elevation, from_spherical_front, from_spherical_side, or from_cylindrical instead. For conversions from or into degree use deg2rad and rad2deg.

Create Coordinates object with or without coordinate points. The points that enter the Coordinates object are defined by the name (domain, convention, and unit. The unit will be deprecated in pyfar v0.8.0 in favor of fixed default units, see Coordinate Systems and Coordinates)

domain, convention	points_1	points_2	points_3	unit
cart, right	x	y	z	met
sph, top_colat	azimuth	colatitude	radius	rad, deg
sph, top_elev	azimuth	elevation	radius	rad, deg
sph, side	lateral	polar	radius	rad, deg
sph, front	phi	theta	radius	rad, deg
cyl, top	azimuth	z	radius_z	rad, deg

Parameters:

points_1 (array like, number) – Points for the first coordinate. 'points_1', 'points_2', and 'points_3' will be renamed to 'x', 'y' and 'z' in pyfar 0.8.0.
points_2 (array like, number) – Points for the second coordinate. 'points_1', 'points_2', and 'points_3' will be renamed to 'x', 'y' and 'z' in pyfar 0.8.0.
points_3 (array like, number) – Points for the third coordinate. 'points_1', 'points_2', and 'points_3' will be renamed to 'x', 'y' and 'z' in pyfar 0.8.0.
domain (string) –
'domain', 'unit' and 'convention' initialization parameters will be deprecated in pyfar 0.8.0 in favor of from_*. Different units are no longer supported. The unit is meter for distances and radians for angles. domain of the coordinate system

'cart'
Cartesian

'sph'
Spherical

'cyl'
Cylindrical

The default is 'cart'.
convention (string) –
'domain', 'unit' and 'convention' initialization parameters will be deprecated in pyfar 0.8.0 in favor of from_*. Different units are no longer supported. Default angle unit is radiant.

Coordinate convention (see above) The default is 'right' if domain is 'cart', 'top_colat' if domain is 'sph', and 'top' if domain is 'cyl'.
unit (string) –
'domain', 'unit' and 'convention' initialization parameters will be deprecated in pyfar 0.8.0 in favor of from_*. Different units are no longer supported. Default angle unit is radiant. The 'deg' parameter will be deprecated in pyfar 0.8.0 in favor of the deg2rad and rad2deg.

Unit of the coordinate system. By default the first available unit is used, which is meters ('met') for domain = 'cart' and radians ('rad') in all other cases (See above).
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
sh_order (int, optional) –
This property will be deprecated in pyfar 0.8.0 in favor of spharpy.samplings.SamplingSphere

Maximum spherical harmonic order of the sampling grid. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Attributes:

`azimuth`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians.
`cartesian`	Returns `x`, `y`, `z`.
`cdim`	Return channel dimension.
`colatitude`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`comment`	Get comment.
`cshape`	Return channel shape.
`csize`	Return channel size.
`cylindrical`	Cylindrical coordinates.
`elevation`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`frontal`	Angle in the y-z plane of the right handed Cartesian coordinate system in radians.
`lateral`	Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians.
`polar`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`radius`	Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).
`rho`	Radial distance to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).
`sh_order`	This function will be deprecated in pyfar 0.8.0 in favor of `spharpy.samplings.SamplingSphere`.
`spherical_colatitude`	Spherical coordinates according to the top pole colatitude coordinate system.
`spherical_elevation`	Spherical coordinates according to the top pole elevation coordinate system.
`spherical_front`	Spherical coordinates according to the frontal pole coordinate system.
`spherical_side`	Spherical coordinates according to the side pole coordinate system.
`upper`	Angle in the x-z plane of the right handed Cartesian coordinate system in radians.
`weights`	Get sampling weights.
`x`	X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).
`y`	Y coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < y < \(\infty\)).
`z`	Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).

Methods:

`copy`()	Return a deep copy of the Coordinates object.
`find_nearest`(find[, k, distance_measure, ...])	Find the k nearest coordinates points.
`find_nearest_cart`(points_1, points_2, ...[, ...])	This function will be deprecated in pyfar 0.8.0 in favor of the `find_within` method.
`find_nearest_k`(points_1, points_2, points_3)	This function will be deprecated in pyfar 0.8.0 in favor of the `find_nearest` method.
`find_nearest_sph`(points_1, points_2, ...[, ...])	This function will be deprecated in pyfar 0.8.0 in favor of the `find_within` method.
`find_slice`(coordinate, unit, value[, tol, ...])	This function will be deprecated in pyfar 0.8.0.
`find_within`(find[, distance, ...])	Find coordinates within a certain distance to the query points.
`from_cartesian`(x, y, z[, weights, comment])	Create a Coordinates class object from a set of points in the right-handed cartesian coordinate system.
`from_cylindrical`(azimuth, z, rho[, weights, ...])	Create a Coordinates class object from a set of points in the cylindrical coordinate system.
`from_spherical_colatitude`(azimuth, ...[, ...])	Create a Coordinates class object from a set of points in the spherical coordinate system.
`from_spherical_elevation`(azimuth, elevation, ...)	Create a Coordinates class object from a set of points in the spherical coordinate system.
`from_spherical_front`(frontal, upper, radius)	Create a Coordinates class object from a set of points in the spherical coordinate system.
`from_spherical_side`(lateral, polar, radius)	Create a Coordinates class object from a set of points in the spherical coordinate system.
`get_cart`([convention, unit, convert])	This function will be deprecated in pyfar 0.8.0 in favor of `cartesian` Get coordinate points in cartesian coordinate systems.
`get_cyl`([convention, unit, convert])	This function will be deprecated in pyfar 0.8.0 in favor of the cylindrical property.
`get_sph`([convention, unit, convert])	This function will be deprecated in pyfar 0.8.0 in favor of the spherical_... properties.
`rotate`(rotation[, value, degrees, inverse])	Rotate points stored in the object around the origin of coordinates.
`set_cart`(x, y, z[, convention, unit])	This function will be deprecated in pyfar 0.8.0 in favor of `cartesian`, `x`, `y` or `z`.
`set_cyl`(azimuth, z, radius_z[, convention, unit])	This function will be deprecated in pyfar 0.8.0 in favor of the `cylindrical` property.
`set_sph`(angles_1, angles_2, radius[, ...])	This function will be deprecated in pyfar 0.8.0 in favor of the `spherical_*` properties.
`show`([mask])	Show a scatter plot of the coordinate points.
`systems`([show, brief])	This function will be deprecated in pyfar 0.8.0, check the documentation instead.

property azimuth#: Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and so on (\(-\infty\) < azimuth < \(\infty\), \(2\pi\)-cyclic).

property cartesian#: Returns x, y, z. Right handed cartesian coordinate system. See see Coordinate Systems and Coordinates for more information.

property cdim#

Return channel dimension.

The channel dimension gives the number of dimensions of the coordinate points excluding the last dimension.

property colatitude#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians colatitude are defined in positive z-direction, \(\pi/2\) radians in positive x-direction, and \(\pi\) in negative z-direction (\(0\leq\) colatitude \(\leq\pi\)). The colatitude is a variation of the elevation angle.

property comment#: Get comment.

copy()[source]#: Return a deep copy of the Coordinates object.

property cshape#

Return channel shape.

The channel shape gives the shape of the coordinate points excluding the last dimension, which is always 3.

property csize#

Return channel size.

The channel size gives the number of points stored in the coordinates object.

property cylindrical#: Cylindrical coordinates. Returns azimuth, z, rho. See see Coordinate Systems and Coordinates for more information.

property elevation#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians elevation are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(-\pi/2\) in negative z-direction (\(-\pi/2\leq\) elevation \(\leq\pi/2\)). The elevation is a variation of the colatitude.

find_nearest(find, k=1, distance_measure='euclidean', radius_tol=None)[source]#

Find the k nearest coordinates points.

Parameters:

find (pf.Coordinates) – Coordinates to which the nearest neighbors are searched.
k (int, optional) – Number of points to return. k must be > 0. The default is 1.
distance_measure (string, optional) –

'euclidean'
distance is determined by the euclidean distance. This is default.

'spherical_radians'
distance is determined by the great-circle distance expressed in radians.

'spherical_meter'
distance is determined by the great-circle distance expressed in meters.
radius_tol (float, None) – For all spherical distance measures, the coordinates must be on a sphere, so the radius must be constant. This parameter defines the maximum allowed difference within the radii. Note that increasing the tolerance decreases the accuracy of the search. The default None uses a tolerance of two times the decimal resolution, which is determined from the data type of the coordinate points using numpy.finfo.

Returns:

index (tuple of arrays) – Indices of the neighbors. Arrays of shape (k, find.cshape) if k>1 else (find.cshape, ).
distance (numpy array of floats) – Distance between the points, after the given distance_measure. It’s of shape (k, find.cshape).

Notes

This is a wrapper for scipy.spatial.cKDTree.

Examples

Find frontal point from a spherical coordinate system

>>> import pyfar as pf
>>> coords = pf.samplings.sph_lebedev(sh_order=10)
>>> to_find = pf.Coordinates(1, 0, 0)
>>> index, distance = coords.find_nearest(to_find)
>>> coords.show(index)
>>> distance
0.0

(Source code, png, hires.png, pdf)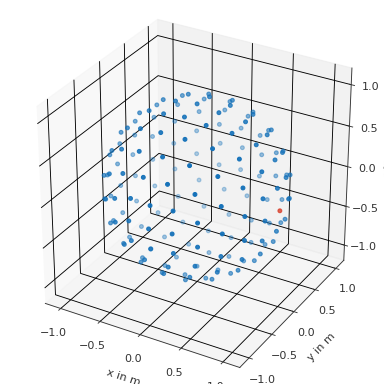

Find multidimensional points in multidimensional coordinates with k=1

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates(np.arange(9).reshape((3, 3)), 0, 1)
>>> to_find = pf.Coordinates(
>>>     np.array([[0, 1], [2, 3]]), 0, 1)
>>> i, d = coords.find_nearest(to_find)
>>> coords[i] == find
True
>>> i
(array([[0, 0],
        [0, 1]], dtype=int64),
 array([[0, 1],
        [2, 0]], dtype=int64))
>>> d
array([[0., 0.],
       [0., 0.]])

Find multidimensional points in multidimensional coordinates with k=3

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates(np.arange(9).reshape((3, 3)), 0, 1)
>>> find = pf.Coordinates(
>>>     np.array([[0, 1], [2, 3]]), 0, 1)
>>> i, d = coords.find_nearest(find, 3)
>>> # the k-th dimension is at the end
>>> i[0].shape
(3, 2, 2)
>>> # now just access the k=0 dimension
>>> coords[i][0].cartesian
array([[[0., 0., 1.],
        [1., 0., 1.]],
       [[2., 0., 1.],
        [3., 0., 1.]]])

find_nearest_cart(points_1, points_2, points_3, distance, domain='cart', convention='right', unit='met', show=False, atol=1e-15)[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the find_within method. Find coordinates within a certain distance in meters to query points.

Parameters:

points_1 (array like, number) – First coordinate of the points to which the nearest neighbors are searched.
points_2 (array like, number) – Second coordinate of the points to which the nearest neighbors are searched.
points_3 (array like, number) – Third coordinate of the points to which the nearest neighbors are searched.
distance (number) – Euclidean distance in meters in which the nearest points are searched. Must be >= 0.
domain (string, optional) – Domain of the points. The default is 'cart'.
convention (string, optional) – Convention of points. The default is 'right'.
unit (string, optional) – Unit of the points. The default is 'met' for meters.
show (bool, optional) – Show a plot of the coordinate points. The default is False.
atol (float, optional) – A tolerance that is added to distance. The default is`` 1e-15``.

Returns:

index (numpy array of ints) – The locations of the neighbors in the getter methods (e.g., cartesian). Dimension as in find_nearest_k. Missing neighbors are indicated with csize. Also see Notes below.
mask (boolean numpy array) – Mask that contains True at the positions of the selected points and False otherwise. Mask is of shape cshape.

Notes

scipy.spatial.cKDTree is used for the search, which requires an (N, 3) array. The coordinate points in self are thus reshaped to (csize, 3) before they are passed to cKDTree. The index that is returned refers to the reshaped coordinate points. To access the points for example use

>>> points_reshaped = self.cartesian.reshape((self.csize, 3))
>>> points_reshaped[index]

Examples

Find frontal points within a distance of 0.5 meters

>>> import pyfar as pf
>>> coords = pf.Coordinates(np.arange(-5, 5), 0, 0)
>>> result = coords.find_nearest_cart(2, 0, 0, 0.5, show=True)

(Source code, png, hires.png, pdf)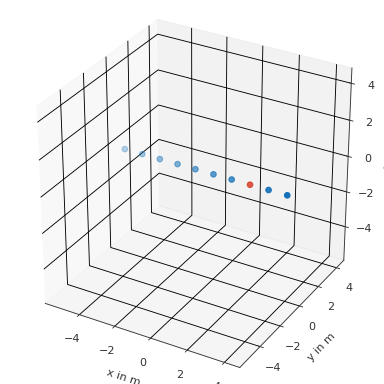

find_nearest_k(points_1, points_2, points_3, k=1, domain='cart', convention='right', unit='met', show=False)[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the find_nearest method.

Find the k nearest coordinates points.

Parameters:

points_1 (array like, number) – First coordinate of the points to which the nearest neighbors are searched.
points_2 (array like, number) – Second coordinate of the points to which the nearest neighbors are searched.
points_3 (array like, number) – Third coordinate of the points to which the nearest neighbors are searched.
k (int, optional) – Number of points to return. k must be > 0. The default is 1.
domain (string, optional) – Domain of the points. The default is 'cart'.
convention (string, optional) – Convention of points. The default is 'right'.
unit (string, optional) – Unit of the points. The default is 'met' for meters.
show (bool, optional) – Show a plot of the coordinate points. The default is False.

Returns:

index (numpy array of ints) – The locations of the neighbors in the getter methods (e.g., self.cartesian). Dimension according to distance (see below). Missing neighbors are indicated with csize. Also see Notes below.
mask (boolean numpy array) – Mask that contains True at the positions of the selected points and False otherwise. Mask is of shape cshape.

Notes

scipy.spatial.cKDTree is used for the search, which requires an (N, 3) array. The coordinate points in self are thus reshaped to (csize, 3) before they are passed to cKDTree. The index that is returned refers to the reshaped coordinate points. To access the points for example use

>>> points_reshaped = self.cartesian.reshape((self.csize, 3))
>>> points_reshaped[index]

Examples

Find the nearest point in a line

>>> import pyfar as pf
>>> coords = pf.Coordinates(np.arange(-5, 5), 0, 0)
>>> result = coords.find_nearest_k(0, 0, 0, show=True)

(Source code, png, hires.png, pdf)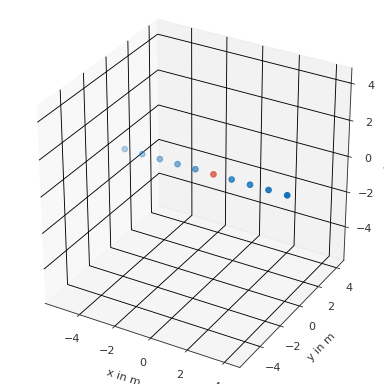

find_nearest_sph(points_1, points_2, points_3, distance, domain='sph', convention='top_colat', unit='rad', show=False, atol=1e-15)[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the find_within method. Find coordinates within certain angular distance to the query points.

Parameters:

points_1 (array like, number) – First coordinate of the points to which the nearest neighbors are searched.
points_2 (array like, number) – Second coordinate of the points to which the nearest neighbors are searched.
points_3 (array like, number) – Third coordinate of the points to which the nearest neighbors are searched.
distance (number) – Great circle distance in degrees in which the nearest points are searched. Must be >= 0 and <= 180.
domain (string, optional) – Domain of the input points. The default is 'sph'.
convention (string, optional) – Convention of the input points. The default is 'top_colat'.
unit (string, optional) – Unit of the input points. The default is 'rad'.
show (bool, optional) – Show a plot of the coordinate points. The default is False.
atol (float, optional) – A tolerance that is added to distance. The default is 1e-15.

Returns:

index (numpy array of ints) – The locations of the neighbors in the getter methods (e.g., cartesian). Dimension as in find_nearest_k. Missing neighbors are indicated with csize. Also see Notes below.
mask (boolean numpy array) – Mask that contains True at the positions of the selected points and False otherwise. Mask is of shape cshape.

Notes

scipy.spatial.cKDTree is used for the search, which requires an (N, 3) array. The coordinate points in self are thus reshaped to (csize, 3) before they are passed to cKDTree. The index that is returned refers to the reshaped coordinate points. To access the points for example use

points_reshaped = points.cartesian.reshape((points.csize, 3)) points_reshaped[index]

Examples

Find top points within a distance of 45 degrees

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates.from_spherical_elevation(
>>>     0, np.arange(-90, 91, 10)*np.pi/180, 1)
>>> result = coords.find_nearest_sph(0, np.pi/2, 1, 45, show=True)

(Source code, png, hires.png, pdf)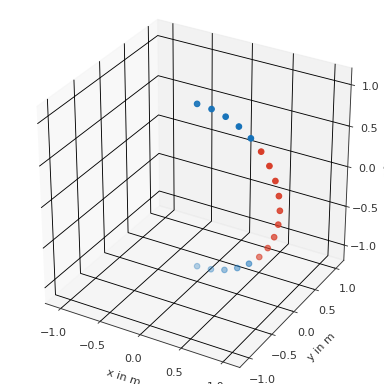

find_slice(coordinate: str, unit: str, value, tol=0, show=False, atol=1e-15)[source]#

This function will be deprecated in pyfar 0.8.0. Use properties and slicing instead, e.g. coords = coords[coords.azimuth>=np.pi].

Find a slice of the coordinates points.

Parameters:

coordinate (str) – Coordinate for slicing.
unit (str) – Unit in which the value is passed
value (number) – Value of the coordinate around which the points are sliced.
tol (number, optional) – Tolerance for slicing. Points are sliced within the range [value-tol, value+tol]. The default is 0.
show (bool, optional) – Show a plot of the coordinate points. The default is False.
atol (number, optional) – A tolerance that is added to tol. The default is 1e-15.

Returns:

index (tuple of numpy arrays) – The indices of the selected points as a tuple of arrays. The length of the tuple matches cdim. The length of each array matches the number of selected points.
mask (boolean numpy array) – Mask that contains True at the positions of the selected points and False otherwise. Mask is of shape self.cshape.

Notes

value must be inside the range of the coordinate (see .systems). However, value +/- tol may exceed the range.

Examples

Find horizontal slice of spherical coordinate system within a ring of +/- 10 degrees

>>> import pyfar as pf
>>> import numpy as np
>>> coords = pf.Coordinates.from_spherical_elevation(
>>>     np.arange(-30, 30, 5)*np.pi/180, 0, 1)
>>> result = coords.find_slice('azimuth', 'deg', 0, 5, show=True)

(Source code, png, hires.png, pdf)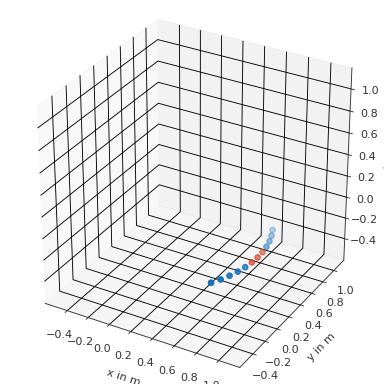

find_within(find, distance=0.0, distance_measure='euclidean', atol=None, return_sorted=True, radius_tol=None)[source]#

Find coordinates within a certain distance to the query points.

Parameters:

find (pf.Coordinates) – Coordinates to which the nearest neighbors are searched.
distance (number, optional) – Maximum allowed distance to the given points find. Distance must be >= 0. For just exact matches use 0. The default is 0.
distance_measure (string, optional) –

'euclidean'
distance is determined by the euclidean distance. This is default.

'spherical_radians'
distance is determined by the great-circle distance expressed in radians.

'spherical_meter'
distance is determined by the great-circle distance expressed in meters.
atol (float, None) – Absolute tolerance for distance. The default None uses a tolerance of two times the decimal resolution, which is determined from the data type of the coordinate points using numpy.finfo.
return_sorted (bool, optional) – Sorts returned indices if True and does not sort them if False. The default is True.
radius_tol (float, None) – For all spherical distance measures, the coordinates must be on a sphere, so the radius must be constant. This parameter defines the maximum allowed difference within the radii. Note that increasing the tolerance decreases the accuracy of the search, i.e., points that are within the search distance might not be found or points outside the search distance may be returned. The default None uses a tolerance of two times the decimal resolution, which is determined from the data type of the coordinate points using numpy.finfo.

Returns:

index – Indices of the containing coordinates. Arrays of shape (find.cshape).

Return type:

tuple of array

Notes

This is a wrapper for scipy.spatial.cKDTree. Compared to previous implementations, it supports self.ndim>1 as well.

Examples

Find all point with 1m distance from the frontal point

>>> import pyfar as pf
>>> coords = pf.samplings.sph_lebedev(sh_order=10)
>>> find = pf.Coordinates(1, 0, 0)
>>> index = coords.find_within(find, 1)
>>> coords.show(index)

(Source code, png, hires.png, pdf)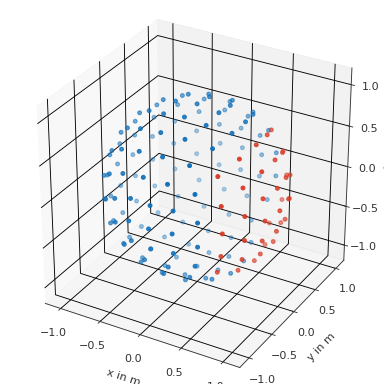

Find all point with 1m distance from two points

>>> import pyfar as pf
>>> coords = pf.Coordinates(np.arange(6), 0, 0)
>>> find = pf.Coordinates([2, 3], 0, 0)
>>> index = coords.find_within(find, 1)
>>> coords.show(index[0])

(Source code, png, hires.png, pdf)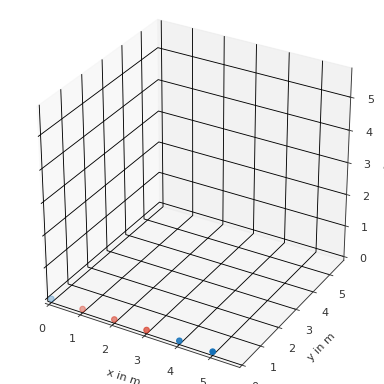

classmethod from_cartesian(x, y, z, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the right-handed cartesian coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

x (ndarray, number) – X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).
y (ndarray, number) – Y coordinate of a right handed Cartesian coordinate system in meters ():math:-infty < y < \(\infty\)).
z (ndarray, number) – Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_cartesian(0, 0, 1)

Or the using init

>>> import pyfar as pf
>>> coordinates = pf.Coordinates(0, 0, 1)

classmethod from_cylindrical(azimuth, z, rho, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the cylindrical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

azimuth (ndarray, double) – Angle in radiant of rotation from the x-y-plane facing towards positive x direction. Used for spherical and cylindrical coordinate systems.
z (ndarray, double) – The z coordinate
rho (ndarray, double) – Distance to origin for each point in the x-y-plane. Used for cylindrical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_cylindrical(0, 0, 1)

classmethod from_spherical_colatitude(azimuth, colatitude, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

azimuth (ndarray, double) – Angle in radiant of rotation from the x-y-plane facing towards positive x direction. Used for spherical and cylindrical coordinate systems.
colatitude (ndarray, double) – Angle in radiant with respect to polar axis (z-axis). Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_colatitude(0, 0, 1)

classmethod from_spherical_elevation(azimuth, elevation, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

azimuth (ndarray, double) – Angle in radiant of rotation from the x-y-plane facing towards positive x direction. Used for spherical and cylindrical coordinate systems.
elevation (ndarray, double) – Angle in radiant with respect to horizontal plane (x-z-plane). Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, float, None, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_elevation(0, 0, 1)

classmethod from_spherical_front(frontal, upper, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

frontal (ndarray, double) – Angle in radiant of rotation from the y-z-plane facing towards positive y direction. Used for spherical coordinate systems.
upper (ndarray, double) – Angle in radiant with respect to polar axis (x-axis). Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_front(0, 0, 1)

classmethod from_spherical_side(lateral, polar, radius, weights: array = None, comment: str = '')[source]#

Create a Coordinates class object from a set of points in the spherical coordinate system. See see Coordinate Systems and Coordinates for more information.

Parameters:

lateral (ndarray, double) – Angle in radiant with respect to horizontal plane (x-y-plane). Used for spherical coordinate systems.
polar (ndarray, double) – Angle in radiant of rotation from the x-z-plane facing towards positive x direction. Used for spherical coordinate systems.
radius (ndarray, double) – Distance to origin for each point. Used for spherical coordinate systems.
weights (array like, number, optional) – Weighting factors for coordinate points. The shape of the array must match the shape of the individual coordinate arrays. The default is None.
comment (str, optional) – Comment about the stored coordinate points. The default is "", which initializes an empty string.

Examples

Create a coordinates object

>>> import pyfar as pf
>>> coordinates = pf.Coordinates.from_spherical_side(0, 0, 1)

property frontal#: Angle in the y-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians frontal angle are defined in positive y-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative y-direction and so on (\(-\infty\) < frontal < \(\infty\), \(2\pi\)-cyclic).

get_cart(convention='right', unit='met', convert=False)[source]#

This function will be deprecated in pyfar 0.8.0 in favor of cartesian Get coordinate points in cartesian coordinate systems.

The points that are returned are defined by the domain, convention, and unit:

domain, convention	p[…,1]	p[…,1]	p[…,1]	units
cart, right	x	y	z	met

For more information run

>>> coords = Coordinates()
>>> coords.systems()

Parameters:

convention (string, optional) – Convention in which the coordinate points are stored. The default is 'right'.
unit (string, optional) – Unit in which the coordinate points are stored. The default is 'met'.
convert (boolean, optional) – If True, the internal representation of the samplings points will be converted to the queried coordinate system. The default is False, i.e., the internal presentation remains as it is.

Returns:

points – Coordinate points. points[...,0] holds the points for the first coordinate, points[...,1] the points for the second, and points[...,2] the points for the third coordinate.

Return type:

numpy array

get_cyl(convention='top', unit='rad', convert=False)[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the cylindrical property. For conversions from or into degree use deg2rad and rad2deg. Get coordinate points in cylindrical coordinate system.

The points that are returned are defined by the domain, convention, and unit:

domain, convention	p[…,1]	p[…,1]	p[…,1]	units
cyl, top	azimuth	z	radius_z	rad, deg

For more information run

>>> coords = Coordinates()
>>> coords.systems()

Parameters:

convention (string, optional) – Convention in which the coordinate points are stored. The default is 'right'.
unit (string, optional) – Unit in which the coordinate points are stored. The default is 'rad'. The 'deg' parameter will be deprecated in pyfar 0.8.0 in favor of the deg2rad and rad2deg.
convert (boolean, optional) – If True, the internal representation of the samplings points will be converted to the queried coordinate system. The default is False, i.e., the internal presentation remains as it is.

Returns:

points – Coordinate points. points[...,0] holds the points for the first coordinate, points[...,1] the points for the second, and points[...,2] the points for the third coordinate.

Return type:

numpy array

get_sph(convention='top_colat', unit='rad', convert=False)[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the spherical_… properties. For conversions from or into degree use deg2rad and rad2deg. Get coordinate points in spherical coordinate systems.

The points that are returned are defined by the domain, convention, and unit:

domain, convention	p[…,1]	p[…,1]	p[…,1]	units
sph, top_colat	azimuth	colatitude	radius	rad, deg
sph, top_elev	azimuth	elevation	radius	rad, deg
sph, side	lateral	polar	radius	rad, deg
sph, front	phi	theta	radius	rad, deg

For more information run

>>> coords = Coordinates()
>>> coords.systems()

Parameters:

convention (string, optional) – Convention in which the coordinate points are stored. The default is 'top_colat'.
unit (string, optional) – Unit in which the coordinate points are stored. The default is 'rad'. The 'deg' parameter will be deprecated in pyfar 0.8.0 in favor of the deg2rad and rad2deg.
convert (boolean, optional) – If True, the internal representation of the samplings points will be converted to the queried coordinate system. The default is False, i.e., the internal presentation remains as it is.

Returns:

points – Coordinate points. points[...,0] holds the points for the first coordinate, points[...,1] the points for the second, and points[...,2] the points for the third coordinate.

Return type:

numpy array

property lateral#: Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and \(-\pi/2\) in negative y-direction (\(-\pi/2\leq\) lateral \(\leq\pi/2\)).

property polar#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians polar angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, \(\pi\) in negative x-direction and so on (\(-\infty\) < polar < \(\infty\), \(2\pi\)-cyclic).

property radius#: Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).

property rho#: Radial distance to the the z-axis of the right handed Cartesian coordinate system (\(0\) < rho < \(\infty\)).

rotate(rotation: str, value=None, degrees=True, inverse=False)[source]#

Rotate points stored in the object around the origin of coordinates.

This is a wrapper for scipy.spatial.transform.Rotation (see this class for more detailed information).

Parameters:

rotation (str) –

'quat'
Rotation given by quaternions.

'matrix'
Rotation given by matrixes.

'rotvec'
Rotation using rotation vectors.

'xyz'
Rotation using euler angles. Up to three letters. E.g., 'x' will rotate about the x-axis only, while 'xz' will rotate about the x-axis and then about the z-axis. Use lower letters for extrinsic rotations (rotations about the axes of the original coordinate system xyz, which remains motionless) and upper letters for intrinsic rotations (rotations about the axes of the rotating coordinate system XYZ, solidary with the moving body, which changes its orientation after each elemental rotation).
value (number, array like) – Amount of rotation in the format specified by rotation (see above).
degrees (bool, optional) – Pass angles in degrees if using 'rotvec' or euler angles ('xyz'). The default is True. Use False to pass angles in radians.
inverse (bool, optional) – Apply inverse rotation. The default is False.

Notes

Points are converted to the cartesian right handed coordinate system for the rotation.

Examples

Get a coordinates object

>>> import pyfar as pf
>>> coords = pf.Coordinates(np.arange(-5, 5), 0, 0)

Rotate 45 degrees about the y-axis using

quaternions

>>> coordinates.rotate('quat', [0 , 0.38268343, 0 , 0.92387953])

a rotation matrix

>>> coordinates.rotate('matrix',
...    [[ 0.70710678,  0 ,  0.70710678],
...     [ 0         ,  1 ,  0.        ],
...     [-0.70710678,  0 ,  0.70710678]])

a rotation vector

>>> coordinates.rotate('rotvec', [0, 45, 0])

euler angles

>>> coordinates.rotate('XYZ', [0, 45, 0])

To see the result of the rotation use

>>> coordinates.show()

set_cart(x, y, z, convention='right', unit='met')[source]#

This function will be deprecated in pyfar 0.8.0 in favor of cartesian, x, y or z. Enter coordinate points in cartesian coordinate systems.

The points that enter the Coordinates object are defined by the domain, convention, and unit

domain, convention	points_1	points_2	points_3	unit
cart, right	x	y	z	met

For more information run

>>> coords = Coordinates()
>>> coords.systems()

Parameters:

x (array like, float) – Points for the first, second, and third coordinate
y (array like, float) – Points for the first, second, and third coordinate
z (array like, float) – Points for the first, second, and third coordinate
convention (string, optional) – Convention in which the coordinate points are stored. The default is 'right'.
unit (string, optional) – Unit in which the coordinate points are stored. The default is 'met' for meters.

set_cyl(azimuth, z, radius_z, convention='top', unit='rad')[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the cylindrical property. For conversions from or into degree use deg2rad and rad2deg. Enter coordinate points in cylindrical coordinate systems.

The points that enter the Coordinates object are defined by the domain, convention, and unit

domain, convention	points_1	points_2	points_3	unit
cyl, top	azimuth	z	radius_z	rad, deg

For more information run

>>> coords = Coordinates()
>>> coords.systems()

Parameters:

azimuth (array like, number) – Counter clock-wise angle in the x-y plane of the right handed Cartesian coordinate system in radians. \(0\) radians are defined in positive x-direction, \(\pi/2\) radians in positive y-direction and so on (\(-\infty\) < azimuth < \(\infty\), \(2\pi\)-cyclic).
z (array like, number) – Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).
radius_z (array like, number) – radius in z plane in meters (\(0\) < radius_z < \(\infty\)).
convention (string, optional) – Convention in which the coordinate points are stored. The default is 'top'.
unit (string, optional) – Unit in which the coordinate points are stored. The default is 'rad'.

set_sph(angles_1, angles_2, radius, convention='top_colat', unit='rad')[source]#

This function will be deprecated in pyfar 0.8.0 in favor of the spherical_* properties. For conversions from or into degree use deg2rad and rad2deg. Enter coordinate points in spherical coordinate systems.

The points that enter the Coordinates object are defined by the domain, convention, and unit

domain, convention	points_1	points_2	points_3	unit
sph, top_colat	azimuth	colatitude	radius	rad, deg
sph, top_elev	azimuth	elevation	radius	rad, deg
sph, side	lateral	polar	radius	rad, deg
sph, front	phi	theta	radius	rad, deg

For more information run

>>> coords = Coordinates()
>>> coords.systems()

Parameters:

angles_1 (array like, number) – Points for the first coordinate, see table above.
angles_2 (array like, number) – Points for the second coordinate, see table above.
radius (array like, number) – Distance to the origin of the right handed Cartesian coordinate system in meters (\(0\) < radius < \(\infty\)).
convention (string, optional) – Convention in which the coordinate points are stored. The default is 'top_colat'.
unit (string, optional) – Unit in which the coordinate points are stored. The default is 'rad'. The 'deg' parameter will be deprecated in pyfar 0.8.0 in favor of the deg2rad and rad2deg.

property sh_order#: This function will be deprecated in pyfar 0.8.0 in favor of spharpy.samplings.SamplingSphere. Get the maximum spherical harmonic order.

show(mask=None, **kwargs)[source]#

Show a scatter plot of the coordinate points.

Parameters:

mask (boolean numpy array, None, optional) – Mask or indexes to highlight. Highlight points in red if mask==True. The default is None, which plots all points in the same color.
kwargs (optional) – Keyword arguments are passed to matplotlib.pyplot.scatter. If a mask is provided and the key c is contained in kwargs, it will be overwritten.

Returns:

ax – The axis used for the plot.

Return type:

Axes3D

property spherical_colatitude#: Spherical coordinates according to the top pole colatitude coordinate system. Returns azimuth, colatitude, radius. See see Coordinate Systems and Coordinates for more information.

property spherical_elevation#: Spherical coordinates according to the top pole elevation coordinate system. azimuth, elevation, radius. See see Coordinate Systems and Coordinates for more information.

property spherical_front#: Spherical coordinates according to the frontal pole coordinate system. Returns frontal, upper, radius. See see Coordinate Systems and Coordinates for more information.

property spherical_side#: Spherical coordinates according to the side pole coordinate system. Returns lateral, polar, radius. See see Coordinate Systems and Coordinates for more information.

systems(show='all', brief=False)[source]#

This function will be deprecated in pyfar 0.8.0, check the documentation instead. Print coordinate systems and their description on the console.

Note

All coordinate systems are described with respect to the right handed cartesian system (domain='cart', convention='right'). Distances are always specified in meters, while angles can be radians or degrees (unit='rad' or unit='deg').

Parameters:

show (string, optional) – 'current' to list the current coordinate system or 'all' to list all coordinate systems. The default is 'all'.
brief (boolean, optional) – Will only list the domains, conventions and units if True. The default is False.

Return type:

Prints to console.

property upper#: Angle in the x-z plane of the right handed Cartesian coordinate system in radians. \(0\) radians upper angle are defined in positive x-direction, \(\pi/2\) radians in positive z-direction, and \(\pi\) in negative x-direction (\(0\leq\) upper \(\leq\pi\)).

property weights#: Get sampling weights.

property x#: X coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < x < \(\infty\)).

property y#: Y coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < y < \(\infty\)).

property z#: Z coordinate of a right handed Cartesian coordinate system in meters (\(-\infty\) < z < \(\infty\)).

pyfar.classes.coordinates.cart2cyl(x, y, z)[source]#

Transforms from Cartesian to cylindrical coordinates.

Cylindrical coordinates follow the convention that the azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation). The height is identical to the z-coordinate and the radius is measured orthogonal from the z-axis.

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}azimuth &= \arctan(\frac{y}{x}),\\height &= z,\\radius &= \sqrt{x^2 + y^2},\end{aligned}\end{align} \]

\[0 < azimuth < 2 \pi\]

Parameters:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z values

Returns:

azimuth (numpy array, number) – Azimuth values
height (numpy array, number) – Height values
radius (numpy array, number) – Radii

Notes

To ensure proper handling of the azimuth angle, the numpy.arctan2 implementation from numpy is used.

pyfar.classes.coordinates.cart2sph(x, y, z)[source]#

Transforms from Cartesian to spherical coordinates.

Spherical coordinates follow the common convention in Physics/Mathematics. The colatitude is measured downwards from the z-axis and is 0 at the North Pole and pi at the South Pole. The azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation).

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}azimuth &= \arctan(\frac{y}{x}),\\colatitude &= \arccos(\frac{z}{r}),\\radius &= \sqrt{x^2 + y^2 + z^2}\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}0 < azimuth < 2 \pi,\\0 < colatitude < \pi\end{aligned}\end{align} \]

Parameters:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z values

Returns:

azimuth (numpy array, number) – Azimuth values
colatitude (numpy array, number) – Colatitude values
radius (numpy array, number) – Radii

Notes

To ensure proper handling of the azimuth angle, the numpy.arctan2 implementation from numpy is used.

pyfar.cross(a, b)[source]#

Cross product of two Coordinates objects.

\[\vec{a} \times \vec{b} = (a_y \cdot b_z - a_z \cdot b_y) \cdot \hat{x} + (a_z \cdot b_x - a_x \cdot b_z) \cdot \hat{y} + (a_x \cdot b_y - a_y \cdot b_x) \cdot \hat{z}\]

Parameters:

a (pf.Coordinates) – first argument, must be broadcastable with b
b (pf.Coordinates) – second argument, much be broadcastable with a

Returns:

result – new Coordinates object with the cross product of the two objects

Return type:

pf.Coordinates

Examples

>>> import pyfar as pf
>>> a = pf.Coordinates(1, 0, 0)
>>> b = pf.Coordinates(0, 1, 0)
>>> result = pf.cross(a, b)
>>> result.cartesian
array([0., 0., 1.])

pyfar.classes.coordinates.cyl2cart(azimuth, height, radius)[source]#

Transforms from cylindrical to Cartesian coordinates.

Cylindrical coordinates follow the convention that the azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation). The height is identical to the z-coordinate and the radius is measured orthogonal from the z-axis.

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}x &= radius \cdot \cos(azimuth),\\y &= radius \cdot \sin(azimuth),\\z &= height\end{aligned}\end{align} \]

\[0 < azimuth < 2 \pi\]

Parameters:

azimuth (numpy array, number) – Azimuth values
height (numpy array, number) – Height values
radius (numpy array, number) – Radii

Returns:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z values

Notes

To ensure proper handling of the azimuth angle, the numpy.arctan2 implementation from numpy is used.

pyfar.deg2rad(coordinates, domain='spherical')[source]#

Convert a copy of coordinates in degree to radians.

Parameters:

coordinates (array like) – N-dimensional array of shape (…, 3).
domain (str, optional) –
Specifies what data are contained in coordinates

'spherical'
Spherical coordinates with angles contained in coordinates[..., 0:2] and radii in coordinates[..., 2]. The radii are ignored during the conversion.

'cylindrical'
Cylindrical coordinates with angles contained in coordinates[..., 0], heights contained in coordinates[..., 1], and radii in coordinates[..., 2]. The heights and radii are ignored during the conversion.

Returns:

coordinates – The converted coordinates of the same shape as the input data.

Return type:

numpy array

pyfar.dot(a, b)[source]#

Dot product of two Coordinates objects.

\[\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z\]

Parameters:

a (pf.Coordinates) – first argument, must be broadcastable with b
b (pf.Coordinates) – second argument, much be broadcastable with a

Returns:

result – array with the dot product of the two objects

Return type:

np.ndarray

Examples

>>> import pyfar as pf
>>> a = pf.Coordinates(1, 0, 0)
>>> b = pf.Coordinates(1, 0, 0)
>>> pf.dot(a, b)
array([1.])

pyfar.rad2deg(coordinates, domain='spherical')[source]#

Convert a copy of coordinates in radians to degree.

Parameters:

coordinates (array like) – N-dimensional array of shape (…, 3).
domain (str, optional) –
Specifies what data are contained in coordinates

'spherical'
Spherical coordinates with angles contained in coordinates[..., 0:2] and radii in coordinates[..., 2]. The radii are ignored during the conversion.

'cylindrical'
Cylindrical coordinates with angles contained in coordinates[..., 0], heights contained in coordinates[..., 1], and radii in coordinates[..., 2]. The heights and radii are ignored during the conversion.

Returns:

coordinates – The converted coordinates of the same shape as the input data.

Return type:

numpy array

pyfar.classes.coordinates.sph2cart(azimuth, colatitude, radius)[source]#

Transforms from spherical to Cartesian coordinates.

Spherical coordinates follow the common convention in Physics/Mathematics. The colatitude is measured downwards from the z-axis and is 0 at the North Pole and pi at the South Pole. The azimuth is 0 at positive x-direction and pi/2 at positive y-direction (counter clockwise rotation).

Cartesian coordinates follow the right hand rule.

\[ \begin{align}\begin{aligned}x &= radius \cdot \sin(colatitude) \cdot \cos(azimuth),\\y &= radius \cdot \sin(colatitude) \cdot \sin(azimuth),\\z &= radius \cdot \cos(colatitude)\end{aligned}\end{align} \]

\[ \begin{align}\begin{aligned}0 < azimuth < 2 \pi\\0 < colatitude < \pi\end{aligned}\end{align} \]

Parameters:

azimuth (numpy array, number) – Azimuth values
colatitude (numpy array, number) – Colatitude values
radius (numpy array, number) – Radii

Returns:

x (numpy array, number) – X values
y (numpy array, number) – Y values
z (numpy array, number) – Z vales